Demo - supplement to some lecture slides
\(\diamondsuit\)Please double click any math symbols to enlarge then a single click will dismiss.
We have learned to take derivative of a function at a point. Now we need to distinguish the following:
Derivative at a point \(x=a\)
\(f'(a)=\lim\limits_{h\to 0}\frac{f(a+h)-f(a)}{h}\)
Derivative as a function (arbitrary points)
\(f'(x)=\lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h}\)
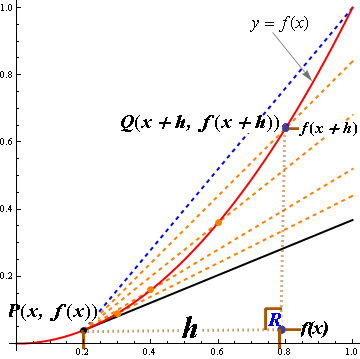
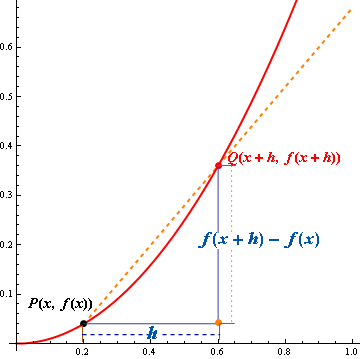
The following may help you to memorize the first principle and the concept of derivative:
- Slope of secant line approaches to slope of the tangent line (see the picture)
- Limit of the ratio of change: \(\frac{\text{Change of } y}{\text{Change of }x } \text{ or use notation } \ \frac{\Delta y}{\Delta x}\) to help you memorize.
Notations for derivative (for a function \(y=f(x)\)):
For the derivative function, we can use any one of the following notations
\(y', \ f'(x),\ \frac{dy}{dx},\ \frac{df}{dx},\ \frac{df(x)}{dx},\ \frac{d}{dx} f(x).\)
For derivative at a particular point \(x=a\), we can use any one of the following notations
\(y'(a),\ y'|_{x=a}, \ f'(a),\ \left.\frac{dy}{dx}\right|_{x=a},\ \left.\frac{df}{dx}\right|_{x=a},\ \left.\frac{df(x)}{dx}\right|_{x=a},\ \left.\frac{d}{dx} f(x)\right|_{x=a}.\)
A further comment:
Around 1950, a MIT Professor, Struik Dirk, taught his student in this way about tangent line:
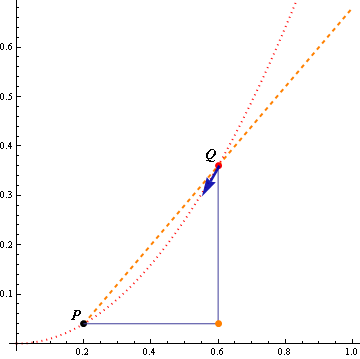
"The tangent passes through two consecutive points of the curve".
As for computer graphics, they consists of pixels, which can be think of as some tiny dots. A secant line passing two adjacent pixels on a curve would be a very good approximation of a tangent line. The following picture will illustrate the idea, if you can imagine that Q approaches to P all the way to the closest dot on the curve (dotted approximation of the continuous curve) .
As an exercise, use the function \(y=x^2\), take a sequence of values in the following as the \(x\) coordinates of the move point Q:
1, 0.8, 0.6, 0.4, 0.3, 0.25, 0.21, 0.201,
then calculate the corresponding \(y\) values and equation of the corresponding secant lines and their slopes. After that, construct a table and observe that the slope of the secant lines indeed approaches to the slope of the tangent line and the derivative \(f'(0.2)\).
If you have any doubts, please contact me or post messages in the topic forum.
______________________________________________________________________________________
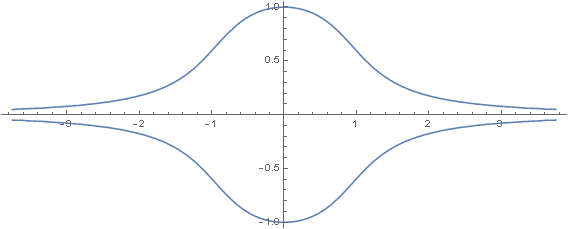
Example (Implicit differentiation):
\(\underline{x^4 y^2}+y^2 \left(x^2+y^2\right)^2=1\). Find the slope of tangent at \(P(0,1)\).
Solution: \(\underline{4x^3y^2+x^4(2y\cdot\frac{dy}{dx})}+2y\cdot\frac{dy}{dx}\cdot \left(x^2+y^2\right)^2+ y^2\cdot 2\left(x^2+y^2\right)\left(2x+2y\frac{dy}{dx}\right)=0\).
\(2x^3y^2+x^4y\cdot\frac{dy}{dx}+y\left(x^2+y^2\right)^2\cdot\frac{dy}{dx}+ 2\left(x^2+y^2\right)y^2\left(x+y\frac{dy}{dx}\right)=0\).
Plug in \(x=0, y=1\) above to get \(\left.\frac{dy}{dx}\right|_{P(0,1)}=0\).
In general, \(2x^3y^2+x^4y\cdot\frac{dy}{dx}+y\left(x^2+y^2\right)^2\cdot\frac{dy}{dx}+ 2xy^2 \left(x^2+y^2\right)+2y^3\left(x^2+y^2\right)\cdot \frac{dy}{dx}=0\).
Solve for \(\frac{dy}{dx}\), get \(\frac{dy}{dx}=-\frac{2xy^2(2x^2+y^2)}{x^4y+y(x^2+y^2)^2+2y^3(x^2+y^2)}\)The picture of the curve looks like this:
.