Examples in complex analysis (includes a MATLAB and MATHEMATICA example))
Completion requirements
Example 1: Compute the integral
\(\int_{\gamma}\frac{z^3+1}{z^3-1}dz,\)
where \(\gamma\) is the curve \(z=e^{it}+e^{4it},t\in[0,2\pi]\).
Hint:
The picture of the curve is shown as follows
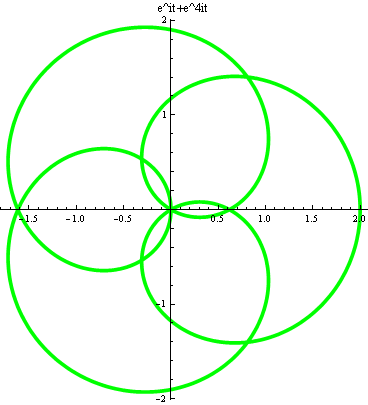
The animation below shows the process from t=0 to \(2\pi\):
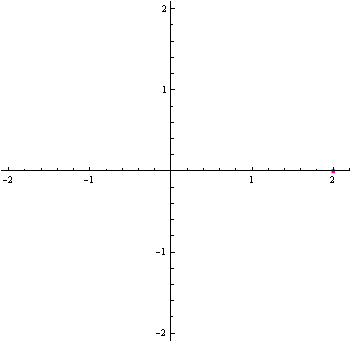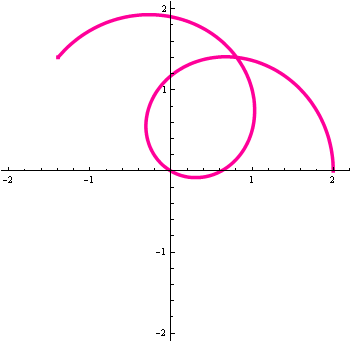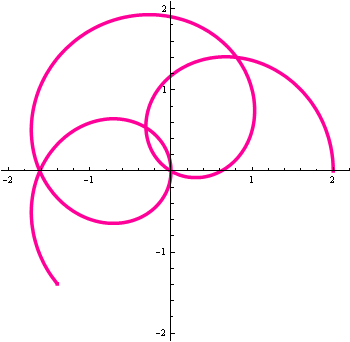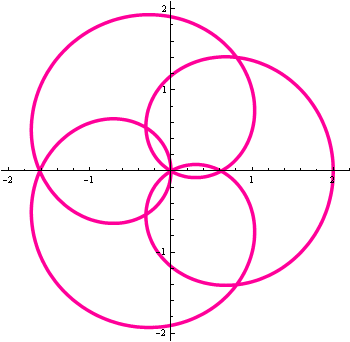
You do not have to plug in \(z=e^{it}+e^{4it},t\in[0,2\pi]\) in order to solve this problem.
Example 2: Evaluate the contour integral
\(\int_{\gamma}\frac{1}{e^z-1}dz,\)where \(\gamma\) is the circle with radius \(3\pi\), centered at \(z=0\), oriented counterclockwise for one loop.
Solution 2: Using Matlab, the code is:
Solution 3: Using Mathematica. \(N\left[3 \pi \int_0^{2 \pi } \frac{i e^{i x}}{-1+e^{3 \pi e^{i x}}} \, dx\right]\) gives an answer: \(0.\, +12.5664 i\). Is this correct? What's wrong?
Last modified: Tuesday, 17 September 2019, 1:29 PM