A few exercises
A few exercises on elementary mathematics
To solve a problem, you need to reduce it to what you already know, convert the original problem into a problem or a few problems that you can solve. This is easier said than done, sometimes. Please analysis the following problems and look at the solutions after you are done or have tried long enough.
All of the following exercises are accessible to high school students.
Exercise 1:
You have $5000 deposited into HSBC tax-free savings account. According to the statistics of the past year, the lowest interest rate for one month is 0.0635662%. So you expect the future monthly interest will be no lower than this. Assuming that your assumption is true and you never withdraw anything out of your account and the interest is compounded once a month. What will you have at the end of 2 the second year?
Exercise 2:
Since you were a child, you have learned what the term ``remainder" means. Give 3 candies to 2 children, each of them must have the same number of candies and we are not allowed to cut any of them. Obviously, you should give each of them one candy, 1 is the remainder. 3 divided by 2, the remainder is 1. In the notation of elementary number theory, we denote this by \(3\equiv 1 (mod 2)\).
(a) Solve \(9x \equiv 1 (mod 17)\) , where \(1\leq x \leq 20\).
(b) Without evaluating \(17^7\), solve \(17^7 \equiv x (mod 41)\), \(x>0\).
Exercise 3:
A prime number normally refer to positive integers other than 1 that have no factors other than 1 and itself, for example, 3,5,7,11, 19, 23, 29, 31, \(\cdots\). Is 2438100000001 a prime number or not? Justify your answer.
Exercise 4:
In the following picture, \(\Delta_{ABC}\) is an equilateral triangle with each side have length 2. What is the biggest figure 8 that you can put inside (in terms of the diameter of the circle)? 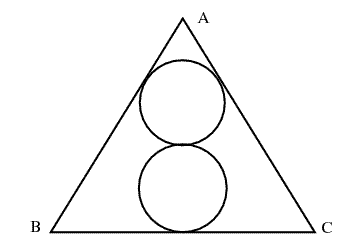
Exercise 5:
Let \(f(x)=x^{4024}-2012x^{2013}+2012x^{2011}-1\). Prove that the graph of \(f(x)\) cross the \(x\)-axis exactly once and find the intersection.