Solutions to exercises
1.
The interest is compounded monthly, 2 years has 24 months, so after 2 years, you will have \(5000(1+0.000635662)^{24}=5076.84\).
So you may earn about $75 dollars in two years. But after two years, inflation make more than the money you have earned. It is possible that two years later, your $5075 can only buy something that cost $4975 two years earlier, especially food or gas, oil. Thus, if you let your money sit in the bank, you are actually losing money!!
The bankers as well as people work at Wall street are much smarter than putting money at a bank to earn interest. You also can be smarter by investing your money is a smarter way than let the banks use your money for their benefits.
If interest you earned is below 10% (APY), it is almost sure that you are losing your money.
2.
(a) There exist integer \(n\), such that
\(9x-1=17n\), so \(x=\frac{17n+1}{9} = \frac{18n+1-n}{9} = 2n
- \frac{n-1}{9}\). \(9|(1-n) \Longrightarrow n = 1, 10\).
Answer is: 2 and 19.
(b)\(17^2=17\times (20 -3) = 340 - 51 = 289 \equiv 2 (mod\ 41)\), so \(17^6 = (17^2)^3 \equiv 2^3 (mod\ 41)\). Thus \(17^7 \equiv 2^3\times 17 (mod\
41)\). The answer is: 13.
3.
The sum of the digits of 24381 is a multiple of 3, so it has factor 3. Repeat this procedure a few times, we can get
\(24381=3^4\times 301 \Rightarrow 2438100000001=3^4\times 301 \times 10^8 +1 = 3^4\times 301 \times 100^4 +1=300^4\times (300+1) +1= 300^5+300^4 +1\).
Now consider whether or not we can factor \(f(x)=x^5+x^4+1\). If we can show that it is not possible to factor this polynomial then we will still have no idea whether or not the number is prime. But if we can factor the polynomial, the the number is not a prime number.
Now we hope that we can factor \(f(x)\). \(f(1)\neq 0, f(-1)=1\neq 0\), so there is no factor of \(f(x)\) in the form of \(ax+b, (b=1)\). Thus, if \(f(x)\) can be factored, it must be of the form
\(x^5+x^4+1=(x^2+ax+1)(x^3+bx^2+cx+1) \mathrm{\ or\ } (x^2+ax-1)(x^3+bx^2+cx-1).\)
Now for the first choice above, expand the right hand side and compare coefficients, we have
\( \left\{ \begin{array}{lcr}
a+b & =& 1\\\\
ab+c+1 & = & 0\\\\
ac+b+1 &=& 0\\\\
a+c &=& 0
\end{array} \right. \)
Solve these equations, we get \(x^5+x^4+1=(x^2+x+1)(x^3-x+1)\). The second choice has no real solution (who cares?).
Thus, plug in \(x=300\), we have \(2438100000001=90301\times 2699970\).
4.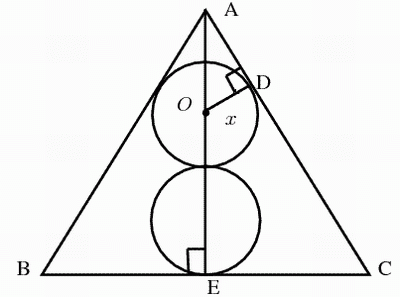
Let the center of the upper circle be O. From O draw a line perpendicular to AC and intersect AC at point D. Let \(|OD|=x\) be the radius of the circle. From \(A\) draw a line that perpendicular to \(BC\) and intersect BC at E.
Now \(\Delta_{ABE}\) and \(\Delta_{ACE}\) share one side and \(|AB|=|AC|\). Also \(\angle B =\angle C\), \(\angle_{AEB}=\angle_{AEC}=90^\circ\), so we have more than enough conditions to claim that \(\Delta_{ABE}\cong\Delta_{ACE}\). Thus \(\angle_{BAE}=\angle_{CAE}=30^\circ\) (because \(\angle{BAC}=60^\circ\)) and \(|BE|=|CE|=1\) (because \(|BC|=2\)). Thus in the right triangle \(\Delta_{AOD}\), we have \(|AO|=2|OD|=2x\). Hence, \(|AE|=2x+x+2x=5x\). Computing \(|AE|\) by using the pythagorean theorem, we have \(|AE|=\sqrt{|AC|^2-|EC|^2}=\sqrt{2^2-1^2}=\sqrt 3\). Thus \(5x=\sqrt 3 \ \Rightarrow \ x=\frac{\sqrt 3}{5}\).
5. Solution available when you enroll a real course.