More problems to exercise your brain ....
Completion requirements
1. Let \(m,n\) be positive integers that satisfy \((m+1)^3-m^3=n^2\). Prove that there exist \(k\in\mathbb{N}\) such that \(k^2+(k+1)^2=n\).
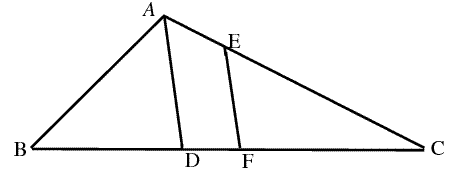
2. In the following picture, AD bisect \(\angle_{BAC}\), |BF|=|FC|, EF parallel to AD. If |AB|=7, |AC|=11, prove that |EC| is an odd integer.
More problems are available in the actual course and you can request for solutions there. You can also post your own problems.
Last modified: Tuesday, 24 July 2012, 9:39 PM