Before investing: Interest and saving (I)
Before investing and trading - savings and calculations
Foreign currency and interest rate
Foreign currency exchange rates can fluctuate wildly, although some have higher interest rates if exchange rates become unfavorable, you may suffer a huge loss.
The foreign currency market is always full of risks due to unexpected events so that 80% or more traders are actually losing money or making almost no profits.
APR and APY - calculate your interest
Assuming the rate is 4.75%. This rate is actually APR - Annual Percentage Rate (simple interest rate before compounding). This rate will normally be compounded every month (we can assume that each month has the same number of days). To do calculations, we need to convert the percentage to 0.0475.
Compounded monthly, that is, each month, your interest rate will be \(\frac{0.0475}{12}\), which is roughly 0.00395833. You do not need a calculator, you can just open Google.com and type in 0.0475/12, the Google will give you the answer.
Suppose initially you have $1000 at the beginning of the year, then after the first month you will have interest \(1000\times\frac{0.0475}{12} = 3.958\). To calculate by using Google, you just type: 1000*(0.0475/12)
So you earned $3.96 for a month. At the end of the first month, you will have \(1000+1000\times\frac{0.0475}{12}\). After you factor the common factor 1000, it is \(1000(1+\frac{0.0475}{12})\), which is roughly 1003.96. Of course, you already know this is just 1000 +3.96, but we are trying to derive a formula and want to see some pattern show up.
In the second month, the interest earned will also earn interest, so your total will be:
\(1000(1+\frac{0.0475}{12}) +1000(1+\frac{0.0475}{12})\times \frac{0.0475}{12}=1000(1+\frac{0.0475}{12})(1+\frac{0.0475}{12})=1000\left(1+\frac{0.0475}{12}\right)^2.\)
Where in the above, we factored out the factor \(1000(1+\frac{0.0475}{12})\) in the first step.
Similarly, by induction, we can get by the end of the year, the total amount will be
\(1000\left(1+\frac{0.0475}{12}\right)^{12}.\)
This is about 1048.55. To use Google, you can simply type 1000*(1+0.0475/12)^(12).
Suppose the currency is AUD and at the beginning of the year the exchange rate is 1:1, and you are using USD. If 1 AUD = 0.95 USD by the end of the year, this will be only 996.12 USD, so by holding AUD you would actually suffer a loss.
In general, the total amount after n months will be \(1000\left(1+\frac{0.0475}{12}\right)^{n}.\)
If \(n\) is the number of years, then the formula should be \(1000\left(1+\frac{0.0475}{12}\right)^{12n}.\)
More generally, if the initial amount is \(p\), APR is \(r\) compounded monthly, then after \(n\) years the total will be
\(p\left(1+\frac{r}{12}\right)^{12n}.\)
Question: How many years are needed for your initial investment to double?
Obviously we need to solve the equation \(p\left(1+\frac{r}{12}\right)^{12n}=2p.\)
\(p \) cancels out, so\(\left(1+\frac{r}{12}\right)^{12n}=2.\)
Now take natural log on both sides to get
\(12n\ln \left(1+\frac{r}{12}\right)=\ln 2.\)
Solve for \(n\), we get
\(n=\frac{\ln 2}{12\ln\left(1+\frac{r}{12}\right)}\)
In the case of our AUD example, plug in \(r\)=0.0475, and we can get the result(use calculator) to be about 14.62 years. So even with this kind of high interest, it takes you about 15 years to double your principal.
Now let's look at the price of silver. The price as of April 21, 2011 is about 46.6 USD. Back a year before, it is about 18 USD even, on April 21, 2010. \(46.6\div 18 = 2.5888\cdots\). That is, the price of silver is about 2.6 times that of a year before, much more than doubled. See the following picture taken from FXCM trading station.
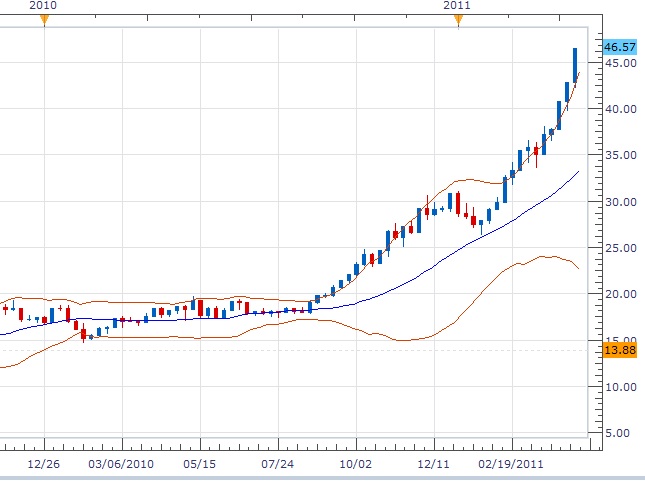
So you can see why doing trading and investing may get higher returns. But the risk of losing all your principal is extremely easy, especially if you use high leverage and do not use good money management skills. In worst cases, you may lose everything you got in a matter of a fraction of a second!
Note: shortly after this article was modified, the silver price went up to 47.66 and then 49.78 USD before it starts to drop and now is at a much lower price.
The next topic will extend on this one and focus on low-risk investments.