Let \(f(x), p(x)\) be two polynomials. Assume that the degree of \(f(x\) is bigger than the degree of \(p(x)\), then we can find a unique quotient (polynomial) \(q(x)\) and a unique remainder polynomial \(r(x)\), such that
\(f(x)=p(x)q(x)+r(x).\)
Question: If \(f(x)=x^3+2x+1, p(x)=x+1\), what is \(q(x)\) and \(r(x)\)?
Answer:
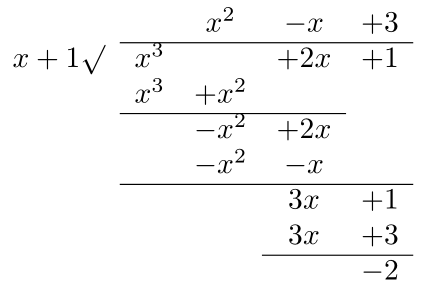
Thus, \(q(x)=x^2-x+3, r(x)=-2 \).